数学之美！

前言

  • 2 个多月前，姜同学问了我一道证明自然数前 项和的公式的题目，也就是自然数幂和公式，让我有了想要重温一下数学的想法。
  • 本文最开始是 版本，后来用 Markdown 完成写作，也提供 PDF 版本(opens new window) 下载， 后续可能会持续更新。
  • 文中选取了一些非常优美的数学公式，并对部分公式加以证明，以此来领略数学的美妙。数学是晦涩难懂的，但又是美丽动人的，实在是难以用言语表达它的美，让人不由感慨数学真是上帝的杰作！

📋 目录

# 1. 自然数幂和公式

自然数平方和

证明

方法一：利用立方差公式累加求和

观察下面的等式：

将以上 个等式相加，左边消去中间项，右边提取公因式合并，得到：

化简整理得到：

方法二：一元函数积分法

构造二次函数：

将区间 分割为 个区间，则每个小曲边三角形的面积为：

所以区间 上 个小矩形面积之和为：

证毕.

自然数立方和

证明

观察下面的等式：

将以上 个等式相加，左边消去中间项，右边提取公因式合并，得到：

化简整理得到：

证毕.

自然数 次幂和公式的规律如下：

# 2. π 和 e

众所周知， 表示圆周率，是最著名的一个无理数。在社交媒体上，每年圆周率日[1]之际，人们总会分享关于 的名言，其中 Lisa Hoffman（丽莎·霍夫曼）的这句算是最为著名的之一了：

Love is like pi —— natural, irrational, and very important.

爱情就像 一样 —— 自然、无理，却至关重要。

可能是受丽莎·霍夫曼这句话的影响，另外一句类似的话也在网络上广为流传，被许多网友在 Twitter(opens new window) 上转发，甚至还被印在 T-shirt(opens new window) 上进行出售：

Love is like pi —— irrational and never-ending.

爱情就像 一样 —— 无理且无穷无尽。

那么 是有多「无理且无穷无尽」呢？下图是「 的足迹」[2]。

100000 位小数的

法国数学家弗朗索瓦·勒·利奥奈（François Le Lionnais）曾说：

Who has not been amazed to learn that the function , like a phoenix rising from its own ashes, is its own derivative?

有谁不被 惊艳过？就像浴火重生的凤凰一般，它从自身的导数中一飞冲天。

一飞冲天

指数函数与对数函数互为反函数，图像关于直线 对称

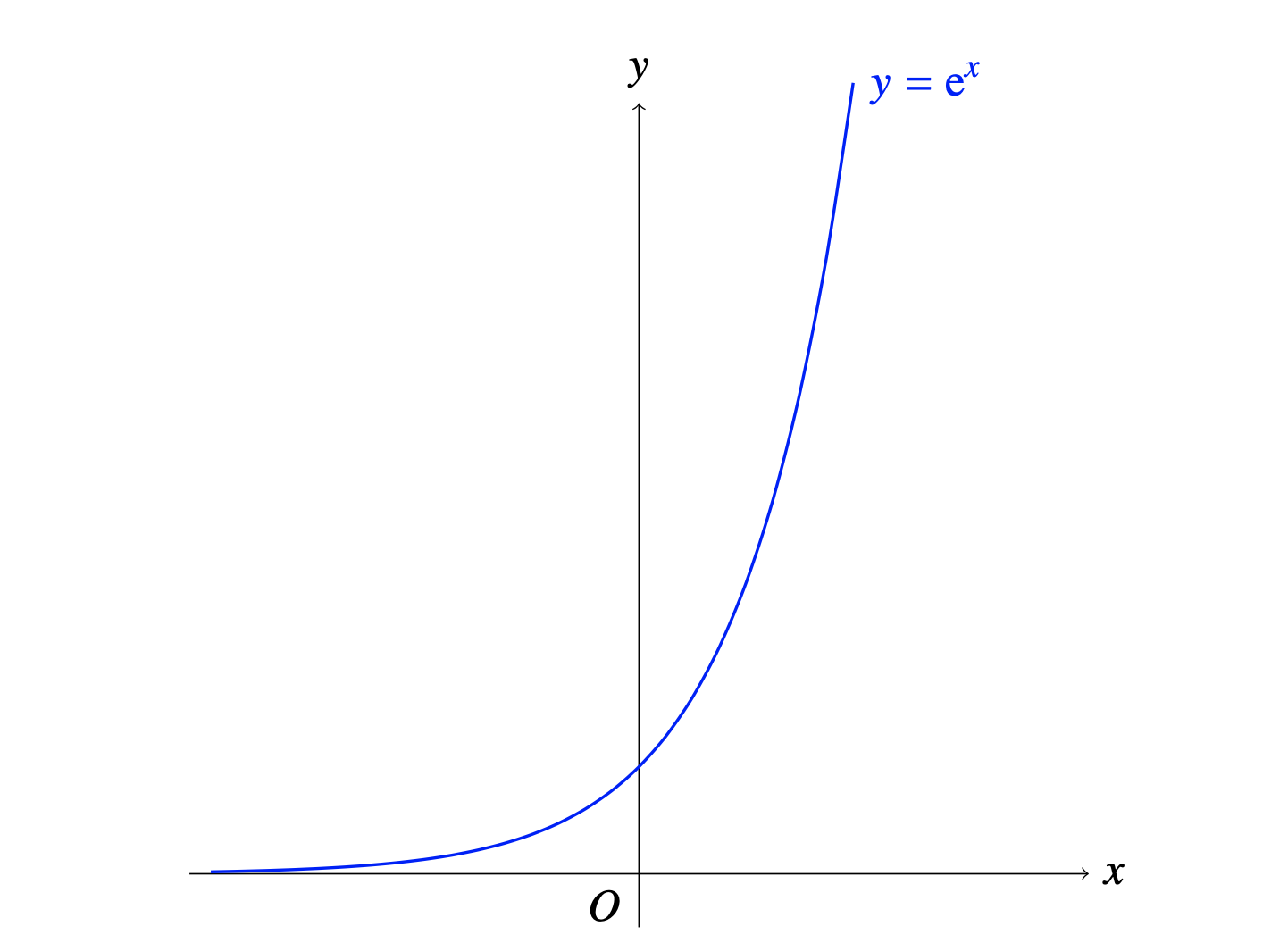
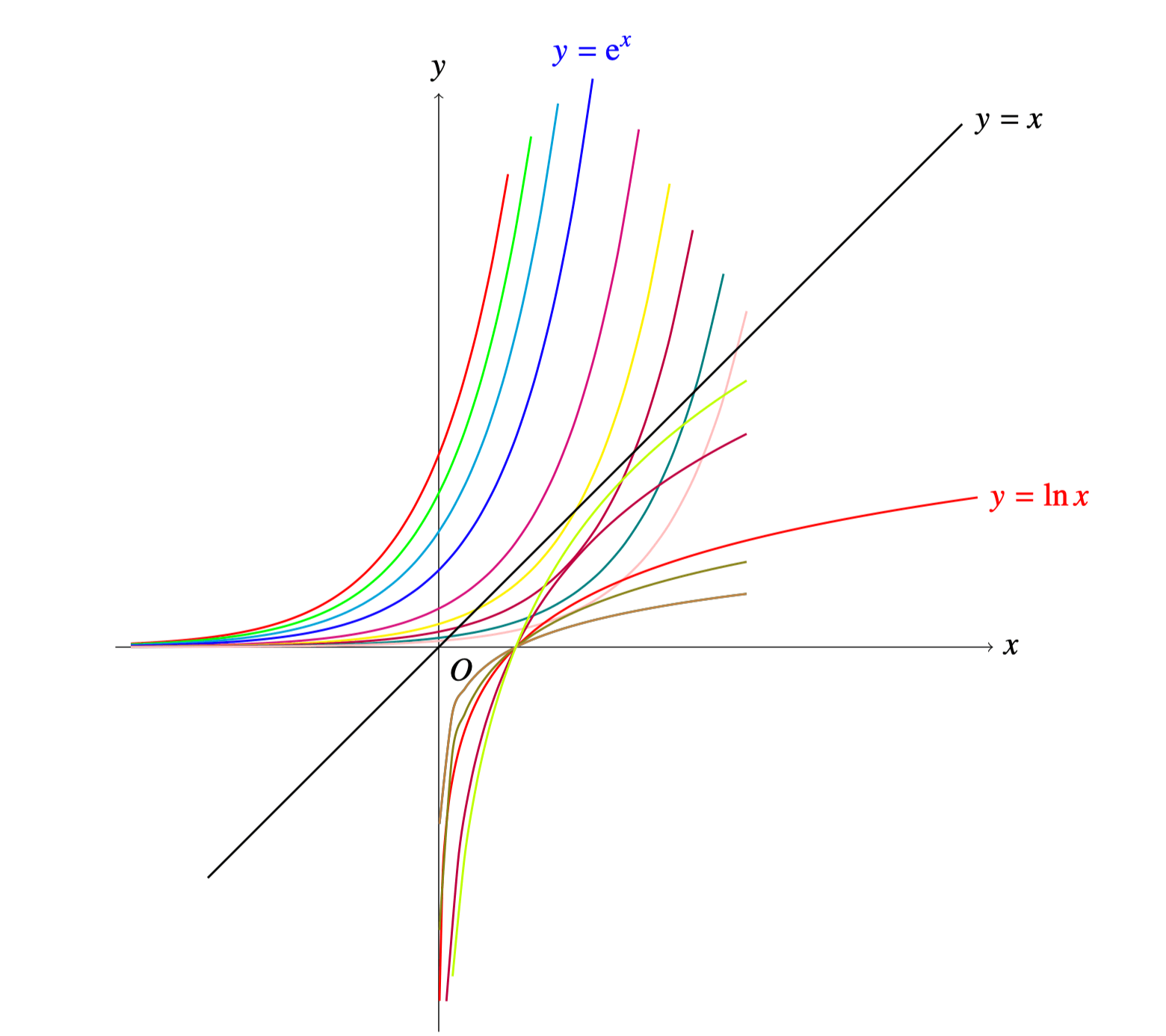
画了上面这幅图，我不禁想起了老何的两首打油诗：

一刀冲天刀未残，接近横轴趋无限。

朵朵菊花集一束，愿留芬芳在人间。

千条万条集一束，左右延伸趋无限。

菊花旋转九十度，指对互为反函数。

和 作为数学界的「无理双雄」，有着千丝万缕的关系，其中，最好吃的是下图这个关系 😋。点击 这里(opens new window) 可下载此图的 PDF 版本。

# 3. π 的莱布尼茨公式

π 的莱布尼茨公式

上式右边的展式是一个无穷级数，被称为莱布尼茨级数，这个级数收敛到 。它通常也被称为格雷戈里-莱布尼茨级数，用以纪念与莱布尼茨同时代的天文学家兼数学家詹姆斯·格雷戈里。

当代有名的数论大家塞尔贝格[3]（Atle Selberg）曾说：

我喜欢数学的一个动机就是因为公式

这个公式实在美极了，单数 这样的组合可以给出 。对于一个数学家来说，此公式正如一幅美丽图画或风景。

证明

而：

根据夹逼定理得：

因此：

证毕.

# 4. 巴塞尔问题

巴塞尔问题

巴塞尔（Basel）城是瑞士的第三大城市，也是欧拉和伯努利家族的故乡。巴塞尔问题是数学史上非常著名的问题，至今还未被证明的黎曼猜想就是在巴塞尔问题的研究基础上提出的，历史上人们对巴塞尔问题有过许多研究，其中最著名的当属大数学家欧拉（Euler）的证明。法国物理学家阿拉果曾如是评价欧拉：

欧拉计算时毫不费力，就像人呼吸、或者鹰在风中保持平衡一样。

以下就是欧拉「毫不费力」的证明～

证明

正弦函数的泰勒级数展开式为：

两边除以 ，得：

当 时， ，我们假设可以把这个无穷级数表示为线性因子的乘积[4]：

把这个乘积展开，并把所有 的项收集在一起，可以看到， 的二次项系数为：

从 原先的级数展开式中可以看出，，因此：

等式两边乘以 ，得出所有平方数的倒数之和：

也即是：

证毕.

关于巴塞尔问题的更多证明方法，可以阅读 巴塞尔问题（Basel problem）的多种解法(opens new window) ，或其 PDF 文件(opens new window) 。

# 5. 欧拉公式

欧拉公式

欧拉公式被称作「上帝公式」或「最伟大的数学公式」，因为它体现了数学的高度统一性，将圆周率 ，自然对数的底数 ，以及 ，， 这 5 个常数如此简洁地统一于一个公式中。事实上，上述公式是公式：

在 时的特例。

欧拉公式虽然被称为「最伟大的公式」，但证明它却并不困难，掌握高等数学中泰勒级数的相关知识即可。

证明

函数 的泰勒级数形式分别为：

将 代入 可得：

于是：

证毕.

# 6. 其他

# 6.1 拉马努金恒等式

拉马努金恒等式

斯里尼瓦瑟·拉马努金（Srinivasa Ramanujan, 1887－1920）是一位印度天才数学家，是亚洲史上最著名的数学家之一。尽管他没有受过正规的高等数学教育，但却沉迷数论，尤爱研究 、质数等数学常数的求和公式，以及整数分拆。惯以直觉导出公式，不喜作证明，而他的理论在后来往往被证明是正确的。

拉马努金一生成就颇丰，提出过很多天才般的等式。可惜天妒英才，健康问题困扰了拉马努金一生，他去世时年仅 33 岁。

2013 年 11 月 4 日，广州恒大微博(opens new window) 曾用拉马努金恒等式预测本队与韩国首尔 FC 亚冠决赛的得分，而对手韩国首尔 FC 的得分则是欧拉公式等号右边的结果 0，即比分为 3-0。最终，广州恒大与首尔 FC 两回合战平 3-3，凭借客场进球制度夺得冠军。

# 6.2 欧拉常数

欧拉常数

欧拉常数是欧拉在 1735 年发现的一个常数，欧拉曾经使用 作为它的符号，并计算出了它的前 6 位小数，意大利数学家洛伦佐·马斯刻若尼引入了 作为这个常数的符号。目前尚不知道该常数是否为有理数。以下是欧拉常数的一些常见积分形式：

欧拉常数常见积分形式

借助欧拉常数，可以轻松证明：

证：记

则有：

由 ，易知也有：

于是：

证毕.

# 6.3 梅钦公式

梅钦公式

# 6.4 斐波那契数列

斐波那契数列

# 6.5 连分数

连分数

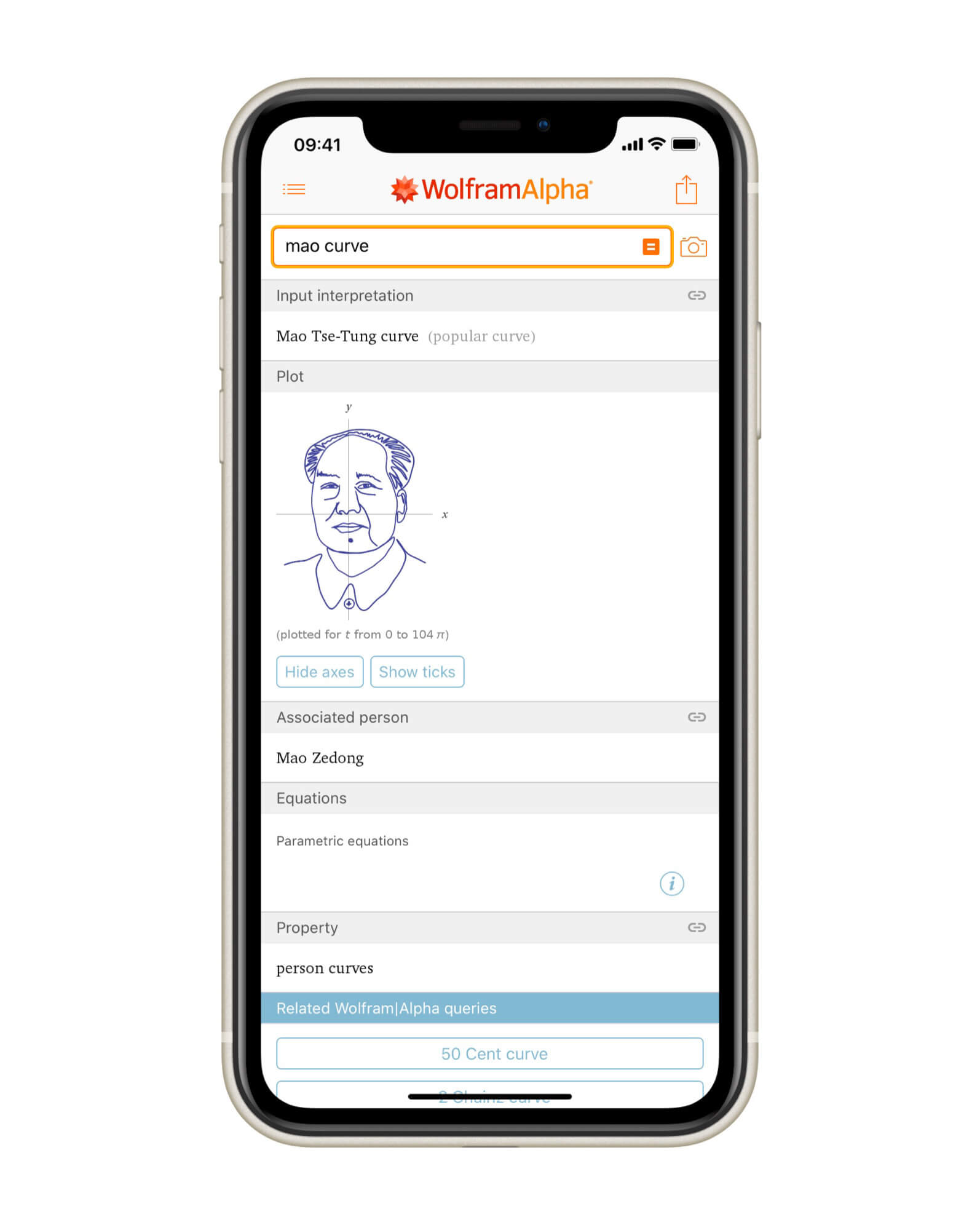
# 6.6 主席函数

「主席函数」这个名字是我起的 😂，是利用三大数学软件之一的 Mathematica，将毛主席的形象用非常复杂的参数方程表示出来。如下图所示，毛泽东的伟岸形象在这里不是普通意义上「画出来」的，而是被视为函数图像（Plot），用一串相当复杂的参数方程表示出来的。

想要知道这个参数方程有多复杂，可前往 WolframAlpha 网页版(opens new window) 查看。当然，你也可以玩玩其他名人的形象，都可以这样表示。如果说前面的公式都体现了一种数学的简洁美，那么「主席函数」就体现了数学无所不能的美！

# § 参考资料

[1] Ian Stewart. In Pursuit of the Unknown: 17 Equations That Changed the World(opens new window) [M]. New York: Basic Books, 2012.

[2] Le Lionnais François. Currents of Mathematical Thought: Mathematics: Concepts and Development(Vol.1)(opens new window) [M]. Mineola: Dover Publications, 2004.

[3] 李长江. 多视角下自然数平方和公式的推导(opens new window) [J]. 中学数学研究（华南师范大学版）, 2015(7):42-44.

[4] 汪晓勤(opens new window) . 欧拉与自然数平方倒数和(opens new window) [J]. 曲阜师范大学学报（自然科学版）, 2002, 28(4):29-33.

[5] 汪晓勤(opens new window) . 谁是幂和公式的开山祖(opens new window) [J]. 科学：上海, 2002, 54(3):53-56.

[6] 吴军. 数学之美(opens new window) [M]. 北京: 人民邮电出版社, 2012.

[7] 蔡天新(opens new window) . 数学传奇：那些难以企及的人物(opens new window) [M]. 北京: 商务印书馆, 2018.

[8] 陈纪修, 於崇华, 金路. 数学分析（第二版）（上册）(opens new window) [M]. 北京: 高等教育出版社, 2004.

[9] 同济大学数学系. 高等数学（第七版）（上册）(opens new window) [M]. 北京: 高等教育出版社, 2014.

[10] 同济大学数学系. 高等数学（第七版）（下册）(opens new window) [M]. 北京: 高等教育出版社, 2014.

  1. 圆周率日（Pi Day）是庆祝圆周率 的特别日子，日期是 3 月 14 日，由圆周率最常用的近似值 3.14 而来。美国麻省理工学院首先倡议将 3 月 14 日定为国家圆周率日（National Pi Day）。2009 年美国众议院正式将每年的 3 月 14 号设定为「圆周率日」（Pi Day）。此外，3 月 14 日也是阿尔伯特·爱因斯坦的生日，卡尔·马克思和史蒂芬·霍金的忌日以及白色情人节。 ↩︎

  2. 不够直观？前往 这里(opens new window) 查看 的动态小数位数，建议使用桌面版 Google Chrome 浏览器，以获得最佳观看体验。 ↩︎

  3. 塞尔贝格，挪威裔美国籍数学家。由于他所做的关于黎曼 函数零点分布问题的出色成果，以及对素数定理的初等证明，于 1950 年荣获 Fields 奖(opens new window) ，时年 33 岁，他还于 1986 年荣获 Wolf 数学奖(opens new window) 。 ↩︎

  4. 欧拉没有严格证明这个无穷积，直到魏尔斯特拉斯得到了他著名的「魏尔斯特拉斯分解定理」（Weierstrass factorization theorem）。 ↩︎